

Tedd próbára a tudásod néhány egyszerű példával!
A legfontosabb összefüggések, összecsomagolva egy helyre!
Kéne egy gyors másodfokú megoldó képlet? Vagy egy gyors kombinatorika számítás? Itt találod!
Napi gyakorlók, kidolgozott feladatok
Szabd személyre az alkalmazást!
@erettmatek
@erettmatek
Ne ess kétségbe! A matematika egy nehéz tantárgy, amivel sokaknak meggyűlik a baja. De biztos vagyok benne, hogy Te is lehetsz belőle ügyes!
Ha úgy érzed, hogy a sulis matekóra kevés, vagy nem az igazi, és már a matekos videóinkat is átrágtad, de még mindig nem kaptál választ a kérdéseidre, ne csüggedj! Néha az embernek szüksége van egy-egy új nézőpontra, hogy minden érthetővé váljon.
Mit szólnál néhány magánórához?
Az ÉrettMatek igazi, 21. századi magánórákat kínál!
Az órákra az otthonod kényelméből is csatlakozhatsz, és rugalmasan választhatsz magadnak időpontot online, így nincs felesleges utazás, telefonálgatás, és hasonlók!
Az ÉrettMatek csapat jelenleg csak a középszintű érettségi szintjéig tart magánórákat, emelt szintű órákat egyelőre nem tartunk.
Az SI rendszer alapegységei és prefixumai
Halmazelmélet, jelölések, halmazműveletek, és azonosságaik
Permutációk, kombinációk, variációk és képleteik
Fontosabb számhalmazok és jelöléseik
Fontosabb oszthatósági szabályok az egész számok körében
Hatványozás művelete és azonosságai
Gyökvonás művelete és azonosságai
Logaritmus művelete és azonosságai
Algebrai kifejezések definíciója, és a legfontosabb azonosságaik
Számtani és mértani sorozatok, kamatos kamat számítása
Gyakori síkidomok kerületének és területének meghatározása
Fontosabb testek felszínének és térfogatának képletei
Ismerkedés a szinusz, koszinusz, tanges, kotangens fogalmával
Szinusztétel, koszinusztétel, tangenstétel, kotangenstétel
Összefüggések trigonometrikus egyenletekhez
Az SI mértékrendszer bevezetésekor 7 alap mennyiség és mértékegység került meghatározásra, ezek az alábbiak:
A halmazokat általában az ábécé nagybetűivel jelöljük, a halmazok elemeinek a jelölésére pedig kisbetűket szoktunk használni.
| a ∈ H | azt jelöli, hogy H jelű halmaznak eleme az a jelű dolog |
|---|---|
| a ∉ H | azt jelöli, hogy H jelű halmaznak nem eleme az a jelű dolog |
| {a1, a2, ... , an} | egy véges halmazt jelöl, melynek elemei a1, a2, ... , an. |
| H := { a∈A | t(a)} | a jelölés azt mutatja, hogy a t tulajdonsággal rendelkező a ∈ A dolgok halmazát jelöljük H-val |
| A = B | azt jelöli, hogy A és B halmaz egyenlő. Két halmaz csak akkor egyenlő, ha elemeik megegyeznek. |
| |A| | az A jelű véges halmaz elemeinek a száma |
| { } vagy Ø | az üres halmaz jelölése |
Az A halmaz akkor részhalmaza a B halmaznak, ha az A halmaz minden eleme megtalálható a B halmazban is.
Jelölése: A ⊂ B vagy B ⊃ A
Az üreshalmaz minden halmaznak részhalmaza. Minden halmaz részhalmaza önmagának.
Az A és B halmaz uniója azokat az elemeket tartalmazza, amelyek az A és a B halmaz közül legalább az egyiknek elemei, vagyis amelyek vagy az A, vagy a B, vagy mindkét halmazban megtalálhatóak.
Jelölése: A U B
Az A és B halmaz metszete azokat az elemeket tartalmazza, amelyek az A és a B halmazban is megtalálhatóak.
Jelölés: A ⋂ B
Az A és B halmaz különbsége azokat az elemeket tartalmazza, amelyek az A halmazban megtalálhatóak, de a B-ben nem.
Jelölés: A \ B
A és B halmaz szimmetrikus különbsége: (A \ B) U (B \ A)
Jelölése: A Δ B
Adott H alaphalmaz, és ennek egy részhalmaza, A. Azokat az elemeket, amik a H halmaznak az elemei, de az A-nak nem, az A halmaz H-ra vonatkozó komplementer halmazának nevezzük.
Jelölés:
Azoknak a rendezett pároknak a halmazát, amelyek első komponense az A halmaz eleme, a második komponense pedig a B halmaz eleme, az A és B halmaz Descartes-féle szorzatának nevezzük.
Jelölés: A x B

Ismétlés nélküli permutáció
n különböző elemet kell sorba rendezni az összes lehetséges módon. Az elrendezések száma:
n!
Ismétléses permutáció
n olyan elemet kell sorba rendezni az összes lehetséges módon, amik között ismétlődő elemek is találhatóak. Ha az ismétlődések számáz k1, k2, ... kr jelölik,
akkor a különböző elrendezések száma: ![]()
Ciklikus permutáció
n különböző elemet kell egy kör mentén sorbarendezni az összes lehetséges módon. Az elrendezések száma:
(n-1)!
Ismétlés nélküli kombináció
n különböző elem közül kell k elemet kiválasztani úgy, hogy egy elemet csak egyszer választhatunk ki, és a kiválasztás sorrendje nem számít. Lehetőségek száma:
![]()
Ismétléses kombináció
n különböző elem közül kell k elemet kiválasztani, a sorrend nem számít, de egy elemet többször is kiválaszthatunk. Lehetőségek száma:
![]()
Ismétlés nélküli variáció
n különböző elem közül kell kiválasztani k elemet, a kiválasztás sorrendje számít, egy elemet csak egyszer lehet kiválasztani. Lehetőségek száma:
![]()
Ismétléses variációk
n különböző elem közül úgy kell k elemet kiválasztani, hogy a kiválasztás sorrendje számít, de egy elemet többször is kiválaszthatunk. Lehetőségek száma:
nk
| N | Természetes számok halmaza - bele tartozik az összes pozitív egész szám |
|---|---|
| Z | Egész számok halmaza - bele tartozik az összes egész szám |
| Q | Racionális számok halmaza - bele tartozik az összes olyan szám, amely felírható két egész szám hányadosaként. Ilyenek az egész számok, a véges tizedes törtek, és a végtelen szakaszos tizedes törtek. |
| Q* | Irracionális számok halmaza - bele tartozik minden olyan szá, amelyek nem racionálisak, azaz a nem szakaszos végtelen tizedes törtek. Ezek a számok nem írhatók fel két egész szám hányadosaként, pl.: π |
| R | Vaós számok - bele tartozik minden racionális és irracionális szám |
Egy b természetes számot akkor nevezünk az a természetes szám osztójának, ha létezik olyan természetes szám, amelyre igaz, hogy a = bc. Köznyelven úgy is megfogalmazhatjuk, hogy egy természetes szám akkor osztója egy másik természetes számnak, ha megvan benne maradék nélkül.
| b | a | b osztója a-nak |
|---|
| 2 | n | ha n utolsó számjegye 0, 2, 4, 6 vagy 8 |
|---|---|
| 5 | n | ha n utolsó számjegye 0 vagy 5 |
| 10 | n | ha n utolsó számjegye 0 |
| 4 | n | ha n utolsó két számjegyéből alkotott szám osztható 4-gyel |
| 8 | n | ha n utolsó három számjegyéből alkotott szám osztható 8-cal |
| 3 | n | ha n számjegyeinek az összege osztható 3-mal |
| 9 | n | ha n számjegyeinek az összege osztható 9-cel |
| 11 | n | ha n számjegyeit összegezzük váltakozó előjellel és az így kapott szám osztható 11-gyel |
Prímszámoknak nevezzük azokat a természetes számokat, amiknek pontosan két osztójuk van.
Bármely 1-nél nagyobb összetett egész szám egyértelműen (azaz a tényezők sorrendjétől eltekintve csak egyféle módon) felbontható prímszámok szorzatára.
Két, vagy több pozitív egész szám legnagyobb közös osztójának jele: ( k ; l )
Két, vagy több pozitív egész szám legkisebb közös többszörösének jele: [ k ; l ]
Ha két pozitív egész számra igaz, hogy a legnagyobb közös osztójuk 1, akkor ez a két szám egymásra vonatkoztatva relatív prímek.
Amennyiben az n pozitív egész szám prímtényezős felbontása az alábbi:
n = p1α1 p2α2 ... pkαk
Akkor n pozitív osztóinak száma:
d(n) = (α1 + 1)(α2 + 1) ... (αk + 1).
Egy a valós szám n-edik (n ≥ 2) hatványa egy olyan n tényezőjű szorzat, amelynek minden tényezője a. a1 = a
Ha a != 0, akkor a0 = 1. A 00 hatványt nem értelmezzük.
Azonos alapú hatványok
Azonos kitevőjű hatványok
A hatvány hatványozása
Az a ≥ 0 szám négyzetgyökének nevezzük azt a nem negatív számot, amely négyzetének értéke a.
ahol n egy 1-nél nagyobb pozitív egész szám
Amennyiben n páros, és a ≥ 0, úgy az n-edik gyök a értéke az a nem negatív szám, amelynek n-edik hatványa a.
Amennyiben n páratlan, és az a tetszőleges valós szám, úgy az n-edik gyök a értéke az a szám, amelynek az n-edik hatványa a.
Azonos alapú gyökök azonosságai
Azonos kitevőjű gyökök azonosságai
További hasznos azonosságok
Egy pozitív valós x szám a alapú (ahol a>0 és a nem 1) logaritmusának azt a hatványkitevőt nevezzük, amelyre a számot emelve x-et kapunk. Jelölése: logax
Az lg x jelölés (egyes területeken log x) egy szám 10-es alapú logaritmusát jelöli.
Az ln x jelölés egy szám e alapú logaritmusát jelöli.
Azonos alapú logaritmus azonosságai
Eltérő alapú logaritmusok kapcsolatai
Azokat a kifejezéseket, amelyek csak számokból, a négy alapműveletből, változókból, és racionális kitevőjű hatványokból állnak, algebrai kifejezéseknek nevezzük. Nem algebrai kifejezés tehát bármi olyan matematikai kifejezés, amiben bármi egyéb (pl. logaritmus, szögfüggvények, stb.) is szerepel.
Legfontosabb azonosságok
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2
a2 - b2 = (a - b)(a + b)
További azonosságok
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a - b)3 = a3 - 3a2b + 3ab2 - b3
A további azonosságok is hamarosan elérhetővé válnak!
A sorozatok olyan függvények, amelyek értelmezési tartománya a pozitív egész számok halmaza, értékkészlete pedig a valós számok halmaza.
A sorozatokat általában kisbetűvel jelöljük, mely mellett alsóindexben szerepel, a tag sorszáma, a b sorozat harmadik tagja tehát a b3 jelet viseli.
A sorozat első n tagjának az összegét az Sn jelöli.
A számtani sorozat a sorozatok egy speciális típusa. Jellemzője, hogy an = an-1 + d, ahol d differencia (különbség) a sorozatra jellemző állandó érték.
an = a1 + (n-1)d
S_n = \frac{a_1 + a_n}{2}\cdot n
A mértani sorozat a sorozatok egy speciális típusa, megynek jellemzője, hogy an = an-1q, ahol q kvóciens (hányados) a sorozatra jellemző állandó érték.
an = a1 + qn-1
S_n = a_1\frac{q^n^-^1}{q-1}
Belső szögek összege: 180 °
Kerület:
K = a + b + c = 2s
Terület:
T = (a * ma) / 2
T = (a * b * sin γ) / 2
T = (a2 * sin ß * sin γ) / 2
T = (abc)/(4R)
Héron-képlet:
s = K/2
T = ![]()
Belső szögek összege: 360 °
Kerület: K = 4a
Terület: T = a2 = d2/2
Belső szögek összege: 360 °
Kerület: K = 2(a + b)
Terület: T = ab
Belső szögek összege: 360 °
Kerület: K = 2(a + b)
Terület: T = ama = ab sin γ
Belső szögek összege: 360 °
Kerület: 4a
Terület: T = am = (ef)/2 = a2 sin γ
Belső szögek összege: 360 °
Kerület: K = a + b + c + d
Terület: T = k * m = ((a+c)/2)*m
Belső szögek összege: 360 °
Kerület: K = 2(a + b)
Terület: T = (ef) / 2
Kerület: K = 2rπ
Terület: T = r2π
Terület: T =abπ
További síkidomok hamarosan!
Felszín: A = 6a2
Térfogat: V = a3
Felszín: A = 2(ab + bc + ca)
Térfogat: V = abc
Felszín: A = 2T + P
ahol a T az alapterület, a P pedig a palást területe
Térfogat: V = Tm
Nézd meg a gúlát 3D-ben!
Felszín: A = T + P
ahol a T az alapterület, a P pedig a palást területe
Térfogat: V = \frac{Tm}{3}
Nézd meg a gúlát 3D-ben!
Felszín: T + t + P
Térfogat: V = \frac{(T+\sqrt{Tt}+t)m}{3}
ahol a T az alaplap területe, a t a fedőlap területe, a P a palást területe, az m pedig a test magassága
más néven körhenger, vagy kör alapú henger
Felszín: A = 2 r^2 \pi + 2r \pi m
Térfogar: V = r^2 \pi m
Más néve körkúp, vagy kör alapú kúp
Felszín: A = r^2 \pi + r \pi a
Térfogat: V = \frac{r^2 \pi m}{3}
Felszín: A = 4R^2 \pi
Térfogat: V = \frac{4R^3 \pi}{3}
További testek hamarosan!
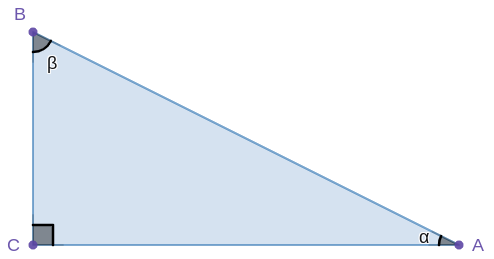
Ne feledd! Ezek az összefüggések csak derékszögű háromszögekben használhatók fel.
sin \alpha = \frac{\text{szöggel szemközti befogó}}{\text{átfogó}}
cos \alpha = \frac{\text{szöggel szomszédos befogó}}{\text{átfogó}}
tg\text{ }\alpha = \frac{\text{szöggel szemközti befogó}}{\text{szöggel szomszédos befogó}}
ctg \alpha = \frac{\text{szöggel szomszédos befogó}}{\text{szöggel szemközti befogó}}
A tangens függvényt a tg jelölésen kívül a tan is jelölheti.
tg\text{ }\alpha = \frac{sin \alpha}{cos \alpha}
ctg \alpha = \frac{cos \alpha}{sin \alpha}
ctg \alpha = \frac{1}{tg\text{ }\alpha}
sin^2\alpha+cos^2\alpha=1
A trigonometrikus tételek nem csak derékszögű, hanem bármilyen háromszögekben működnek.
Egy háromszög oldalainak hossza úgy aránylik egymáshoz, mint a velük szemközti szögek szinusza.
a : b : c = sin \alpha : sin \beta : sin \gamma
\frac{a}{sin \alpha} = \frac{b}{sin \beta} = \frac{c}{sin \gamma}
Ha háromszög két oldalának négyzetéből kivonjuk az általuk bezárt szög koszinuszának, valamint a két oldal hosszának a szorzatának a dupláját, megkapjuk a háromszög harmadik oldalának négyzetét.
c^2 = a^2 + b^2 - 2ab cos \gamma
\frac{a-b}{a+b}=\frac{tg\frac{\alpha-\beta}{2}}{tg\frac{\alpha+\beta}{2}}
ctg \frac{\alpha}{2} = \frac{s - a}{p}
ctg \frac{\beta}{2} = \frac{s - b}{p}
ctg \frac{\gamma}{2} = \frac{s - c}{p}
ahol...
p = \sqrt{\frac{(s-a)(s-b)(s-c)}{s}}
s = \frac{a + b + c}{2}
Az alábbi összefüggések mindegyike esetén a k-val jelölt szám egész szám. Ezt a feladatok megoldásakor jelölni is szükséges.
sin \alpha = sin (\alpha + 2k\pi) \text{ és } sin \alpha = sin (\pi-\alpha + 2k\pi)
cos \alpha = cos (\alpha + 2k\pi) \text{ és } cos \alpha = cos (-\alpha + 2k\pi)
tg \alpha = tg (\alpha + k\pi)
ctg \alpha = ctg (\alpha + k\pi)
Nullára rendezett másodfokú egyenlet megoldása.
Szám összes osztója, prím-e a szám?
Ismétléses és ismétlés nélküli kombináció
Adj meg egy számot:
Ez a szám
Ennek a számnak osztója van.
A szám osztói:
Add meg a másodfokú egyenletet:
x2 + x + = 0
A diszkrimináns értéke:
Az egyenletnek .
Az egyenlet megoldása(i):
$d = #calcMasodfokuB*#calcMasodfokuB - 4*#calcMasodfokuA*#calcMasodfokuC; #calcMasodfokuDisc=$d; if($d < 0) { #calcMasodfokuIndok = "nincs megoldása"; #calcMasodfokuMegoldas = "nincs"; }; if($d == 0) { #calcMasodfokuIndok = "egy megoldása van"; #calcMasodfokuMegoldas = (0-#calcMasodfokuB+sqrt($d))/(2*#calcMasodfokuA); }; if($d > 0) { #calcMasodfokuIndok = "két megoldása van"; #calcMasodfokuMegoldas = ((0-#calcMasodfokuB+sqrt($d))/(2*#calcMasodfokuA))." és ".((0-#calcMasodfokuB-sqrt($d))/(2*#calcMasodfokuA)); };Add meg az adatokat a számításhoz!
n =
k =
Ismétlés nélküli kombináció:
Ismétléses kombináció: .
#calcKombinacioNelkuli = ceil((#calcKombinacioN!)/(#calcKombinacioK! * (#calcKombinacioN - #calcKombinacioK)!)) ; $newN = #calcKombinacioN + #calcKombinacioK - 1; $newK = #calcKombinacioK; #calcKombinacioIsmetleses = ceil(($newN!)/($newK! * ($newN - $newK)!)) ;Érts meg új témaköröket kidolgozott feladatainkkal!
Hamarosan érkeznek a további eszközök!
Elérkezett az ideje a gyakorlásnak? Ide kattintva indíthatod is az új gyakorlást!
Ügyes vagy! Már perce gyakorolsz! Már csak perc hogy elérd a mostanra kitűzött célod.
Ha úgy érzed, hogy végeztél mostanra, nyomd meg az alábbi gombot, hogy lezárd a gyakorlást, és bekerüljön a naplódba.
az elmúlt 15 napban
Tűzz ki célokat, hogy motiváld magad a tanulásra!
A legutóbbi néhány gyakorlás...
Mielőtt belevágnál a mai matekozásba, íme néhány tanács, amik segíthetnek a hatékony munkában!
1. Felszerelés
Előkészítettél mindent, amikre szükséged lehet a tanuláshoz? (íróeszköz, füzet, könyvek, esetleg függvénytáblázat és számológép?)
2. Környezet
Elpakoltad a felesleges dolgokat a környezetedből? Minél több a felesleges dolog a környezetedben, annál könnyebben terelődhet el a figyelmed a gyakorlásról.
3. Célok
4. Mehetünk?
Ha úgy érzed, készen állsz, akkor nyomj az alábbi gombok egyikére, és sok sikert kívánok a gyakorláshoz!
Előkészültem, kezdem a tanulást!
Válassz magadnak célokat a matematika tanuláshoz, gyakorláshoz! A céljaidat később a gyakorlósegédben követheted majd nyomon.

Jó tanulást!
A célodig hátra van: 12:00 perc
Ha úgy érzed, hogy elkalandoztak a gondolataid, nyomd meg a lentebbi gombot.
Úgy érzem, elterelődtek a gondolataim
Ha használni szeretnéd az appot tanulás közben, itt visszatérhetsz.
Végeztél a tanulással? Zárd le a gyakorlást!
Jelöld meg, hogy mi terelte el a figyelmedet a tanulásról. Így pontosabb tanácsokat tudunk adni, hogy hogyan lehetsz hatékonyabb!
Mozgáshiányom van, nem tudok nyugodtan ülni
Mozgáshiányom van, nem tudok nyugodtan ülni
Nem bírom ki a kütyüim nélkül
Nem bírom ki a kütyüim nélkül
Nem bírom ki a kütyüim nélkül
Más terelte el a figyelmem
Gratulálok, végeztél a gyakorlással! Válaszolj néhány kérdésre, hogy reflektálj a mai munkádra!
Az alábbi dobozban számokat látsz 1-től 30-ig. Jelöld be a számokat növekvő sorrendben! Próbáld meg minél gyorsabban megtalálni a következőt.
Ide tudod kidolgozni a megoldásodat. :)
Írd ide a matekot:
Kaptál, vagy nyertél valamilyen különleges tananyagot az egyik promóciónkon? Ezeket itt találod.
Köszönjük, hogy kipróbálod a ZsebMatek appot! Kövesd az utasításokat a képernyő alján, hogy telepíthesd!

Köszönjük, hogy kipróbálod a ZsebMatek appot!
Az applikáció telepítéséhez nyisd meg a böngésződ menüjét a ... gombbal, majd válaszd az Alkalmazás telepítése vagy Hozzáadás a kezdőképernyőhöz feliratú gombot.
Köszönjük, hogy kipróbálod a ZsebMatek appot!
Ahhoz, hogy telepíthesd a PWA-nkat, először nyisd meg ezt az oldalt a mobilkészüléked böngészőjében!
Vagy ha a gomb nem működik, csak keresd fel a telefonod böngészőjében a zsebmatek.qrapp.hu linket. (iPhone esetén Safarit, android esetén a Chrome-ot javasoljuk)
Köszönjük, hogy kipróbálod a ZsebMatek appot!
Sajnos az Instagram, Facebook, stb. beépített böngészőablakából nem lehet feltelepíteni ezt az appot. De ne csüggedj, segítünk! Nincs más dolgod, mint megnyitni ezt az oldalt a telefonod normál böngészőjében!
Ezt megteheted a jobb felső sarokban a ... menüből, vagy csak másold ki az alábbi hivatkozást a vágólapra:
https://zsebmatek.qrapp.hu/
Majd nyisd meg a telefonod böngészőjét (iPhone esetén Safarit, android esetén a Chrome-ot javasoljuk), és keresd fel benne a kimásolt linket!
Így máris telepítheted a ZsebMatek-ot a telefonodra! Jó tanulást!